第二話

• BEGAN:Boundary Equilibrium Generative Adversarial Networksを読んだ時の話

挨拶

G : 今週のヤンジャンはGWのため、お休みでした。どうも泣きそうなguguchiです。

M : guguchiによると今週ヤンジャン休みみたいです。悔しいです。masoです。

G : 今週は1ヶ月くらい前にバズっていたBEGAN:Boundary Equilibrium Generative Adversarial Networks（以下、BEGAN）を読んでいきたいと思います。

会話

G : まず概要について説明します。BEGANは、discriminatorにauto-encoderを使って、生成モデルの再構成誤差の分布と真の分布の再構成誤差の分布のWasserstein距離を小さくしようという論文です。特徴は、従来のmin-maxの定式化ではなく、２つの目的関数を最小化するという定式化になっている所ですね。論文中のリザルトの生成された顔画像は、エグいぐらいすごいリアリティーがありますね。

M : 俺ちょっとこの論文意味分かんないんだけど。。。

G : masoさん、僕もめっちゃ意味わかんないとこありました。

M : やっぱり？とりあえず、論文中の式見ていきましょう！

G : そうですね！まずは、discriminatorが$\theta_D$でパラメトライズされたauto-encoderになっていて、再構成誤差は

$$L(x; \theta_D) = \|x - D(x)\|^2_2$$

で計算されます。

M : Gをgeneratorとすると、この手法のdiscriminatorの目的は、$L(x; \theta_D)$は0に近づける。一方で$L(G(z); \theta_D)$と$L(x; \theta_D)$のWasserstein距離を遠ざけることだね。

G : そうです。ここで一つの仮定が入ります。それは、真の分布・生成モデルの再構成誤差の分布がそれぞれ

$$L(x; \theta_D) \sim \mathcal{N}(m_1 , C_1)$$ $$L(G(z) ; \theta_D) \sim \mathcal{N}(m_2 , C_2)$$

になるという仮定です。

M : 論文中では、”We found experimentally, for the datasets we tried, the loss distribution is, in fact, approximately normal.”って言ってますね。この仮定を使うと、ガウシアンのWasserstein距離が解析的に計算できるという性質が使えます。すると

$$W(\mu_1, \mu_2) = \|m_1 - m_2 \|_2^2 + trace(C_1 + C_2 - 2C_2^{1/2} C_1 C_2^{1/2})^{1/2})$$

が導けます。さらに次元が１次元の場合は、

$$W(\mu_1, \mu_2) = \|m_1 - m_2 \|_2^2 + (c_1 + c_2 - 2 \sqrt{c_1 c_2})$$

で計算できます。

G : そうですね。ここでもう１つ僕的によくわかんない仮定が入ります。$\frac{c_1 + c_2 - 2 \sqrt{c_1 c_2}}{\|m_1 - m_2 \|_2^2}$が定数になるという仮定です。masoさんこれって大丈夫なんですか？

M : 平均が小さかい時はバリアンスも小さい、平均が大きい時はバリアンスも大きいっていうのはそんなにおかしくないんじゃない？

G : まぁ、そうか。。。

M : 本当にやばいのは論文の3.2からだよ。

G : そうなんですね。3.2では、まず再構成誤差の分布のWasserstein距離をどうやってでかくするかについて述べています。再構成誤差のWasserstein距離を大きくする方法は

$$\begin{align} (a) \begin{cases} W(\mu_1,\mu_2) \propto m_1 - m_2 \\ m_1 \to \infty\\ m_2 \to 0\\ \end{cases} (b) \begin{cases} W(\mu_1,\mu_2) \propto m_2 - m_1 \\ m_1 \to 0\\ m_2 \to \infty\\ \end{cases} \end{align}\$$

(a)と(b)の２つがあると言っています。ただ真の分布の再構成誤差$L(x)$は0になって欲しい。つまり、(b)の場合を選択すると言ってます。この場合、２つの目的関数をminimizationするという定式化ができるらしく、

$$\begin{align} \mathcal{L}_D &= L(x;\theta_D) - L(G(z;\theta_G);\theta_D)\\ \mathcal{L}_G &= L(G(z;\theta_G);\theta_D)\\ \end{align}\ $$

になると言っています。

M : 今まではDでW距離を大きくして、GでW距離を小さくしてたけど、これって逆じゃない？ちょっと可視化してしてみよう！

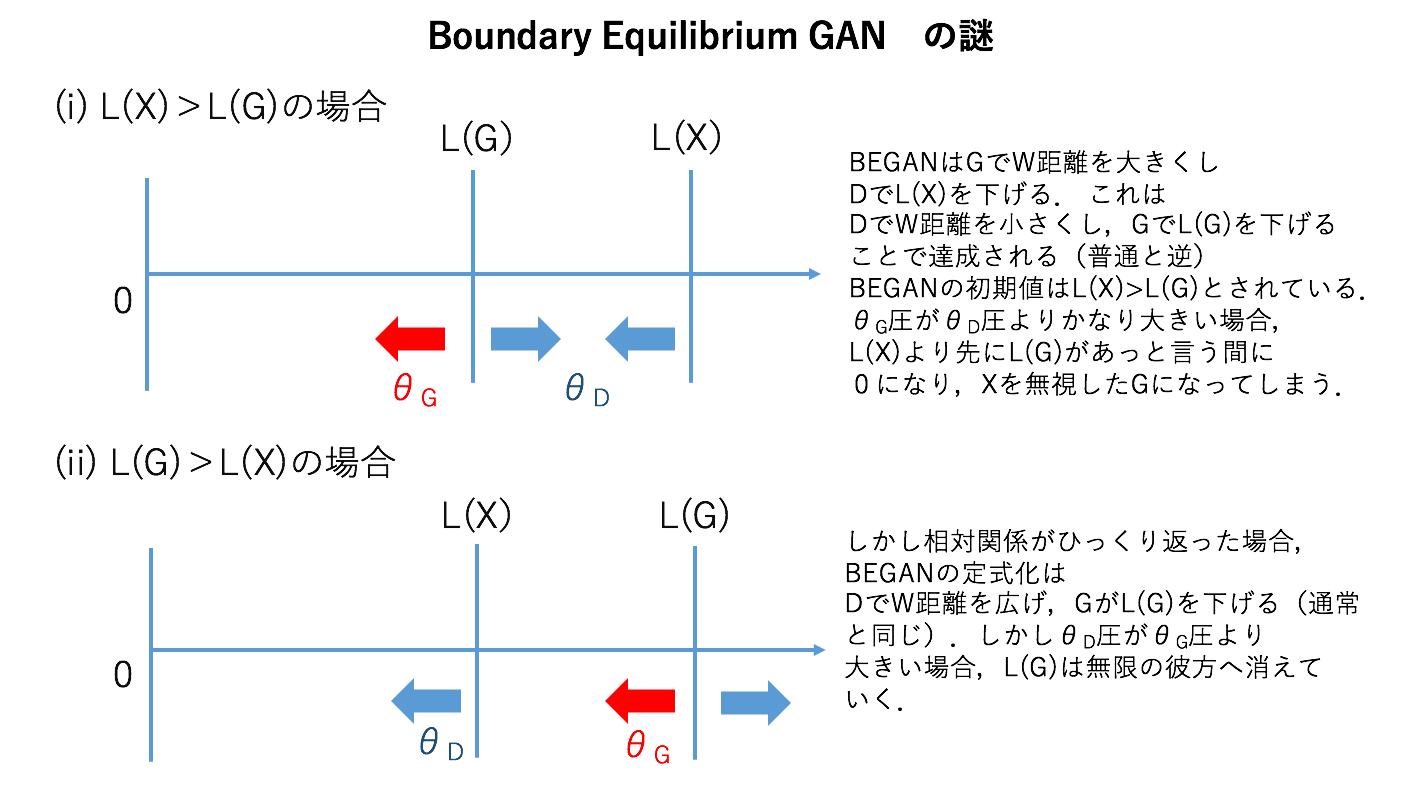
G : $L(G)$が$L(x)$より大きい時は、今まで通りみたいですね。

M : でも、学習初期では$L(x)>L(G)$って書いてたね。

In early training stages, G tends to generate easy-to-reconstruct data for the auto-encoder since generated data is close to 0 and the real data distribution has not been learned accurately yet. This yields to L(x) > L(G(z))

(i)$L(x)>L(G)$の場合は、 $L(G)$があっという間に0になってしまわないか？ここすごい気持ち悪い。guguchiが前の記事で言ってたmin-maxとmax-minの問題に戻ってくる気がする。というのも、最悪のdiscrimiantorに耐えるようなgeneratorを作るのがGANの正当性だった。この正当性の観点から言うと、$L(x)$についてくるように$L(G)$を誘導するのが目指すべき目的だ。でも、定式化は$L(G)$が0に近づいていくから初めて$L(x)$が0に近づける。$L(G)$これって本末転倒じゃん。変なことが起きそう。

G : じゃあ$L(G)$が$L(x)$より先に0にならないためには、$\theta_D$の最適化のスピードが$\theta_G$の最適化のスピードが速くないといけない。すると$L(x)$が$L(G)$を追い越して、(ii)$L(x)< L(G)$になる。この場合は、$\theta_D$の最適化のスピードが$\theta_G$の最適化のスピードが速いと、$L(G)$が無限の彼方に吹っ飛んでしまう。だから、(ii)$L(x)< L(G)$では、$\theta_G$の最適化のスピードが$\theta_D$の最適化のスピードが速くないといけない。つまり、(i)$L(x)> L(G)$から(ii)$L(x)< L(G)$へ移った時、$\theta_D$の最適化のスピードと$\theta_G$の最適化のスピードの大小関係が入れ替わって欲しい感じになってますね。

M : でも、3.3 Equilibriumを見るに、その追い越しが起きないように制御工学を使って

$$\frac{E[L(G)] }{E[L(X)]}$$

$\gamma$になるように調整してるよね。しかもこれ、$L(G)$が先に0にならないようにする調整も担ってるっぽいね。

G : それって、この式のことですか？

$$\begin{align} \mathcal{L}_D &= L(x) - k_t \cdot L(G(z_D))\\ \mathcal{L}_G &= L(G(z_G))\\ k_{t+1} &= k_t + \lambda_k(\gamma L(x) - L(G(z_D)) \end{align}\ $$

この式は、追い越しをなくす効果はなくないですか？

M : あぁそうだね。 $e = \gamma L(x) - L(G(z_D)$とすると、$e$が大きい時は、$L(G)$を小さすぎる。だから$k$を大きくして$L(x)$について来させる。$e$がマイナスになったり、0に近くなってWasserstein距離の計算で使われた’ratio’が不安定になりそうになったら、$k$を小さくしてる。

G : 結局これって、入れ替わりが頻繁に起こるから、学習はめっちゃ不安定になりそうですね。再現実験してる記事何個か見ましたけど、学習めっちゃ大変そうでした。これのせいなんですかね？(musyokuさんの記事 , underfittingさんの記事 , rcallandさんのgithub）

D : $L(x)$と$L(G)$の軌道を見てみたいね。上手くいかない場合と上手くいく場合どんな違いがあるんだろう？

G : 乞うご期待!!!（GPUがなくて死ぬ音）

M : Give me Grants…